Differences between revisions 72 and 81 (spanning 9 versions)
⇤ ← Revision 72 as of 2011-02-07 05:25:44 →
Size: 13648
Editor: jgalaz
Comment:
← Revision 81 as of 2023-09-29 12:51:26 → ⇥
Size: 13375
Editor: SteveLudtke
Comment:
Deletions are marked like this. Additions are marked like this.
Line 1: Line 1:
## page was renamed from Eman2TransformInPython
Line 11: Line 12:
We use the [[http://blake.bcm.edu/eman2/doxygen_html/classEMAN_1_1Transform.html|Transform]] class for storing/managing Euler angles,translations, scales and x mirroring. At any time a Transform object {{{$$Tr$$}}} defines a group of 4 transformations of a rigid body that are applied in a specific order, namely

{{{$$ Tr \equiv M T S R $$}}}

Where {{{$$M$$}}} is a mirroring operation about the x-axis, {{{$$T$$}}} is a translation, {{{$$S$$}}} is a uniform, positive, non zero scaling operation and {{{$$R$$}}} is a rotation. The Transform object stores these transformations internally in a 3x4 matrix, which appears as

{{{$$ Tr = [sMR,M\mathbf{t}]$$}}}

Where {{{$$s$$}}} is the constant scaling factor, {{{$$M$$}}} is the identity or the x-mirroring matrix, {{{$$R$$}}} is a {{{$$3x3$$}}} rotation matrix and {{{$$\mathbf{t}=(tx,ty,tz)^T$$}}} is the translation.		 We use the [[http://blake.bcm.edu/doxygen/classEMAN_1_1Transform.html|Transform]] class for storing/managing Euler angles,translations, scales and x mirroring. At any time a Transform object {{{Tr}}} defines a group of 4 transformations of a rigid body that are applied in a specific order, namely

{{{ Tr = M T S R }}}

Where {{{M}}} is a mirroring operation about the x-axis, {{{T}}} is a translation, {{{S}}} is a uniform, positive, non zero scaling operation and {{{R}}} is a rotation. The Transform object stores these transformations internally in a 3x4 matrix.
Line 24: Line 21:
||EMAN ||$$phi$$, Alt, Az ||{{{$$ [[cos phi,sin phi, 0],[-sin phi,cos phi,0],[0,0,1]] [[1,0,0],[0, cos al, sin al],[0, -sin al, cos al]] [[cos az,sin az, 0],[-sin az,cos az,0],[0,0,1]] $$}}} ||
||Imagic ||$$gamma$$, $$beta$$, $$alpha$$ ||{{{$$ [[cos gamma,sin gamma, 0],[-sin gamma,cos gamma,0],[0,0,1]] [[1,0,0],[0, cos beta, sin beta],[0, -sin beta, cos beta]] [[cos alpha,sin alpha, 0],[-sin alpha,cos alpha,0],[0,0,1]] $$}}} ||
||Spider ||$$psi$$, $$theta$$, $$phi$$ ||{{{$$ [[cos psi,sin psi, 0],[-sin psi,cos psi,0],[0,0,1]] [[cos theta,0,sin theta],[0, 1, 0],[-sin theta, 0, cos theta]] [[cos phi,sin phi, 0],[-sin phi,cos phi,0],[0,0,1]] $$}}} ||
||MRC ||$$psi$$, $$theta$$, $$Omega$$ ||{{{$$ [[cos psi,sin psi, 0],[-sin psi,cos psi,0],[0,0,1]] [[cos theta,0,sin theta],[0, 1, 0],[-sin theta, 0, cos theta]] [[cos Omega,sin Omega, 0],[-sin Omega,cos Omega,0],[0,0,1]] $$}}} ||
||XYZ ||z, y, x ||{{{$$ [[cos z,sin z, 0],[-sin z, cos z,0],[0,0,1]] [[cos y,0,sin y],[0, 1, 0],[-sin y, 0, cos y]] [[1,0,0],[0, cos x, sin x],[0, -sin x, cos x]] $$}}} ||
||spin ||$$Omega$$, n1, n2, n3 ||Quaternion rotation by $$ Omega $$ degrees about the vector $$[n1,n2\,n3]$$ ||
||sgirot ||q, n1, n2, n3 ||Quaternion rotation by q degrees about the vector $$[n1,n2\,n3]$$ ||
||quaternion ||e0, e1, e2, e3 ||Literal quaternion rotation using $$ q = e0 + e1\mathbf{i} + e2\mathbf{j} + e2\mathbf{k} $$ ||

 ||EMAN ||az, alt, phi (Z,X,Z') ||{{{ [[cos phi,sin phi, 0],[-sin phi,cos phi,0],[0,0,1]] [[1,0,0],[0, cos al, sin al],[0, -sin al, cos al]] [[cos az,sin az, 0],[-sin az,cos az,0],[0,0,1]] }}} ||
||Imagic ||gamma, beta, alpha ||{{{ [[cos gamma,sin gamma, 0],[-sin gamma,cos gamma,0],[0,0,1]] [[1,0,0],[0, cos beta, sin beta],[0, -sin beta, cos beta]] [[cos alpha,sin alpha, 0],[-sin alpha,cos alpha,0],[0,0,1]] }}} ||
||Spider ||psi, theta, phi ||{{{ [[cos psi,sin psi, 0],[-sin psi,cos psi,0],[0,0,1]] [[cos theta,0,sin theta],[0, 1, 0],[-sin theta, 0, cos theta]] [[cos phi,sin phi, 0],[-sin phi,cos phi,0],[0,0,1]] }}} ||
||MRC ||phi, theta, omega ||{{{ [[cos phi,sin phi, 0],[-sin phi,cos phi,0],[0,0,1]] [[cos theta,0,sin theta],[0, 1, 0],[-sin theta, 0, cos theta]] [[cos omega,sin omega, 0],[-sin omega,cos omega,0],[0,0,1]] }}} ||
||XYZ ||z, y, x ||{{{ [[cos z,sin z, 0],[-sin z, cos z,0],[0,0,1]] [[cos y,0,sin y],[0, 1, 0],[-sin y, 0, cos y]] [[1,0,0],[0, cos x, sin x],[0, -sin x, cos x]] }}} ||
||spin ||Omega, n1, n2, n3 ||Quaternion rotation by Omega degrees about the vector [n1,n2\,n3] ||
||sgirot ||q, n1, n2, n3 ||Quaternion rotation by q degrees about the vector [n1,n2\,n3] ||
||quaternion ||e0, e1, e2, e3 ||Literal quaternion rotation using q = e0 + e1\mathbf{i} + e2\mathbf{j} + e2\mathbf{k} ||
||2d||alpha||Rotation in 2-D only, for 3-D objects this is a rotation about Z||
Line 160: Line 156:
e.proceess_inplace("xform",{"transform":t})
}}}
In fact {{{e.transform(t)}}} actually calls {{{e.proceess_inplace("math.transform",{"transform":t})}}} internally on the C++ side.		 e.process_inplace("xform",{"transform":t})
}}}
In fact {{{e.transform(t)}}} actually calls {{{e.process_inplace("xform",{"transform":t})}}} internally on the C++ side.
Line 227: Line 223:
As stated previously, {{{e.transform(t)}}} actually calls {{{e.proceess_inplace("math.transform",{"transform":t})}}} internally on the C++ side. As stated previously, {{{e.transform(t)}}} actually calls {{{e.process_inplace("xform",{"transform":t})}}} internally on the C++ side.

Contents

  1. The center of the image
  2. What is a Transform?
  3. Supported Rotation Conventions
  4. The Transform object in Python
    1. Constructing a Transform
    2. Setting/getting rotations
    3. Setting/getting scale
    4. Setting/getting mirror
    5. Setting/getting translation
    6. Setting/getting parameters
    7. A Transform multiplied by a Vec3f
    8. Transforming a 3D image
  5. 2D degenerate use of the Transform object in Python
    1. Setting/getting 2D rotations
    2. Setting/getting 2D translation
    3. Setting/getting 2D parameters
    4. A Transform multiplied by a Vec2f
    5. Transforming a 2D image
  6. A more in depth look at the dictionary constructor
  7. A more in depth look at set_params
    1. If unspecified, old parameters are retained
    2. For rotation and translation, setting one is equivalent to setting them all

The center of the image

The center of the image for purposes of rotations is different for odd and even sized images. For even images, the center is at (nx/2,ny/2) where the first pixel is at (0,0). For odd sized images, the center is at ((nx-1)/2,(ny-1)/2). The same concept extends to 3-D.

center1.png center2.png

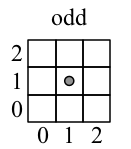
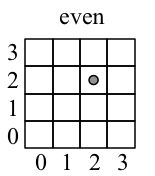
What is a Transform?

We use the Transform class for storing/managing Euler angles,translations, scales and x mirroring. At any time a Transform object Tr defines a group of 4 transformations of a rigid body that are applied in a specific order, namely

 Tr = M T S R 

Where M is a mirroring operation about the x-axis, T is a translation, S is a uniform, positive, non zero scaling operation and R is a rotation. The Transform object stores these transformations internally in a 3x4 matrix.

Supported Rotation Conventions

Convention

Angle Names

Matrices

EMAN

az, alt, phi (Z,X,Z')

 [[cos phi,sin phi, 0],[-sin phi,cos phi,0],[0,0,1]] [[1,0,0],[0, cos al, sin al],[0, -sin al, cos al]] [[cos az,sin az, 0],[-sin az,cos az,0],[0,0,1]] 

Imagic

gamma, beta, alpha

 [[cos gamma,sin gamma, 0],[-sin gamma,cos gamma,0],[0,0,1]] [[1,0,0],[0, cos beta, sin beta],[0, -sin beta, cos beta]] [[cos alpha,sin alpha, 0],[-sin alpha,cos alpha,0],[0,0,1]] 

Spider

psi, theta, phi

 [[cos psi,sin psi, 0],[-sin psi,cos psi,0],[0,0,1]] [[cos theta,0,sin theta],[0, 1, 0],[-sin theta, 0, cos theta]] [[cos phi,sin phi, 0],[-sin phi,cos phi,0],[0,0,1]] 

MRC

phi, theta, omega

 [[cos phi,sin phi, 0],[-sin phi,cos phi,0],[0,0,1]] [[cos theta,0,sin theta],[0, 1, 0],[-sin theta, 0, cos theta]] [[cos omega,sin omega, 0],[-sin omega,cos omega,0],[0,0,1]] 

XYZ

z, y, x

 [[cos z,sin z, 0],[-sin z, cos z,0],[0,0,1]] [[cos y,0,sin y],[0, 1, 0],[-sin y, 0, cos y]] [[1,0,0],[0, cos x, sin x],[0, -sin x, cos x]] 

spin

Omega, n1, n2, n3

Quaternion rotation by Omega degrees about the vector [n1,n2\,n3]

sgirot

q, n1, n2, n3

Quaternion rotation by q degrees about the vector [n1,n2\,n3]

quaternion

e0, e1, e2, e3

Literal quaternion rotation using q = e0 + e1\mathbf{i} + e2\mathbf{j} + e2\mathbf{k}

2d

alpha

Rotation in 2-D only, for 3-D objects this is a rotation about Z

The Transform object in Python

Constructing a Transform

There a four ways to construct a Transform object in Python 

   1 t = Transform() # default constructor, t is the identity
   2 t = Transform({"type":"eman","az":10,"alt":150,"scale":2.0,"mirror":True,"tx":3.4}) # construction using a dictionary
   3 p = Transform({"type":"eman","az":10,"mirror":True,"tx":3.4}) # construction using a dictionary
   4 q = Transform([1,0,0,0,0,1,0,0,0,0,1,0]) # specify the 12 entries of the matrix explicitly, row wise (3 rows of 4)
   5 s = Transform(t) # copy construction - s is precisely the same as t

NOTE: All the CONVENTIONS listed on the table above can be supplied as arguments or "values" for the "type" key in the Transform's dictionary. For example: 

   1 t = Tranform({"type":"spin"})
   2 t = Tranform({"type":"quaternion"})
   3 t = Tranform({"type":"imagic"})
   4 Etc.

For more information on default parameters and what happens when some parameters are not set see a more in depth look at the dictionary constructor

Setting/getting rotations

   1 t = Transform()
   2 t.set_rotation({"type":"spider","phi":32,"theta":12,"psi":-100})
   3 spider_rot = t.get_rotation("spider")
   4 eman_rot = t.get_rotation("eman")
   5 s = Transform(eman_rot) # works fine

NOTE: The get_rotation() method can take a string as an argument, but it does NOT require one; it is defaulted to 'eman'. That is, it will return the rotation of the transform object in 'eman' convention. You can supply ANY rotation CONVENTION as a string to get the rotation in the corresponding convention, irrespective of the "type" you set for the transform. For example, from an 'eman' type Transform, 

   1 t = Transform({'type':'eman'})

You can still get the rotation in other conventions: 

   1 t.get_rotation('spin') gives {'Omega': 0.0, 'n1': 0.0, 'n2': 0.0, 'n3': 0.0, 'type': 'spin'}
   2 t.get_rotation('quaternion') gives  {'e0': 1.0, 'e1': 0.0, 'e2': 0.0, 'e3': 0.0, 'type': 'quaternion'}

Setting/getting scale

   1 t = Transform()
   2 t.set_scale(2.0)
   3 scale = t.get_scale()
   4 s = Transform({"scale":scale}) # set scale as part of construction

Setting/getting mirror

   1 t = Transform()
   2 #  Can be set using integers
   3 t.set_mirror(1) # means True
   4 t.set_mirror(0) # means False
   5 t.set_mirror(False)
   6 t.set_mirror(True)
   7 mirror = t.get_mirror()
   8 s = Transform({"mirror":mirror}) # set mirror as part of construction

Setting/getting translation

   1 t = Transform()
   2 t.set_trans(1,2,3) # method 1
   3 t.set_trans(Vec3f(1,2,3)) # method 2
   4 t.set_trans([1,2,3]) # method 3 - the tuple is converted to a Vec3f automatically
   5 v = t.get_trans()
   6 s = Transform({"tx":v[0],"ty":v[1],"tz":v[2]}) # set translation as part of construction

Setting/getting parameters

You can tell a Transform deduce any of its parameters from a dictionary. Similarly you can get the parameters of a Transform as a dictionary 

   1 t = Transform()
   2 t.set_params({"type":"eman","az":10,"alt":150,"scale":2.0,"mirror":True,"tx":3.4})
   3 d = t.get_params("eman") # must specify the euler convention
   4 s = Transform(d) # s is the same as t
   5 d = t.get_params("spider")
   6 s = Transform(d) # s is the same as t
   7 d = t.get_params("matrix")
   8 s = Transform(d) # s is the same as t

For more information the behaviour of set_params see a more in depth look at set_params

A Transform multiplied by a Vec3f

The transformation of a 3D vector $$ v = (v_x,v_y,v_z)^T $$ by a Transform is defined as

$$ Tr \mathbf{v}  = [sMR,M\mathbf{t}] (v_x,v_y,v_z,1)^T = sMR\mathbf{v}+ M\mathbf{t}  $$

This can be done in Python using the following 

   1 t = Transform()
   2 t.set_params({"type":"eman","az":10,"alt":150,"scale":2.0,"mirror":True,"tx":3.4})
   3 v = Vec3f(3,4,10)
   4 v_transformed = t*v
   5 v_transformed = t.transform(v) # can also do it this way if you prefer

Transforming a 3D image

Transforming a 3D image is achieved using a single function call 

   1 t = Transform()
   2 t.set_params({"type":"eman","az":10,"alt":150,"scale":2.0,"mirror":True,"tx":3.4})
   3 t.set_trans( ... )
   4 e = test_image_3d()
   5 e.transform(t)

You can alternatively use the EMData processing framework, for example: 

   1 t = Transform()
   2 t.set_params({"type":"eman","az":10,"alt":150,"scale":2.0,"mirror":True,"tx":3.4})
   3 t.set_trans( ... )
   4 f = e.process("xform",{"transform":t}) # memory efficient
   5 e.process_inplace("xform",{"transform":t})

In fact e.transform(t) actually calls e.process_inplace("xform",{"transform":t}) internally on the C++ side.

2D degenerate use of the Transform object in Python

The Transform object can be used as though it were a 2D transformation matrix. In this case the interface for setting/getting scale and mirror is unchanged. However setting the rotation should be done using the euler type "2d", and there are some accommodations for setting and getting 2d translations and parameters.

Setting/getting 2D rotations

Use the "2d" euler type, and the angle is specified using "alpha" 

   1 t = Transform()
   2 t.set_rotation({"type":"2d","alpha":32})
   3 a = t.get_rotation("2d")
   4 s = Transform(a) # works fine

Setting/getting 2D translation

The interface is more or less identical to the 3D case 

   1 t = Transform()
   2 t.set_trans(1,2) # method 1
   3 t.set_trans(Vec2f(1,2)) # method 2
   4 v = t.get_trans_2d()
   5 s = Transform("tx":v[0],"ty",v[1]) # set translation as part of construction

Setting/getting 2D parameters

For getting the parameters in 2D form use the following 

   1 t = Transform()
   2 t.set_params({"type":"2d","alpha":10,"scale":2.0,"mirror":True,"tx":3.4,"ty":0.0}) # no special interface required for 2D, use the same as 3D
   3 d = t.get_params("2d")
   4 s = Transform(d) # s is the same as t

A Transform multiplied by a Vec2f

The transformation of a 2D vector $$ v_{2D} = (v_x,v_y)^T $$ by a Transform is equivalent to setting the z component of 3D vector to 0. If $$ v = (v_x,v_y,0)^T $$ then the 2D transformation is equivalent to the following,

$$ Tr \mathbf{v_{2D}}  = [sMR,M\mathbf{t}] (v_x,v_y,0,1)^T = sMR\mathbf{v}+ M\mathbf{t}  $$

and the z component is ignored. Note that the internal implementation is efficient. 2D vector transformation can be done in Python using the following 

   1 t = Transform()
   2 t.set_params({"type":"2d","alpha":10,"scale":2.0,"mirror":True,"tx":3.4})
   3 v = Vec2f(3,1)
   4 v_transformed = t*v
   5 v_transformed = t.transform(v) # can also do it this way if you prefer

Transforming a 2D image

Transforming a 2D image is achieved using a single function call 

   1 t = Transform()
   2 t.set_params({"type":"2d","alpha":10,"scale":2.0,"mirror":True,"tx":3.4})
   3 e = test_image()
   4 e.transform(t)

You can alternatively use the EMData processing framework, for example: 

   1 t = Transform()
   2 t.set_params({"type":"2d","alpha":10,"scale":2.0,"mirror":True,"tx":3.4})
   3 f = e.process("xform",{"transform":t}) # memory efficient
   4 e.proceess_inplace("xform",{"transform":t})

As stated previously, e.transform(t) actually calls e.process_inplace("xform",{"transform":t}) internally on the C++ side.

Note that if you try to transform a 2D image using a Transform that contains 3D rotations or translations you will get an error: 

   1 t = Transform({"type":"eman","alt":22}) # 3D rotation
   2 a = test_image() # 2D
   3 a.transform(t) # ERROR is thrown
   4 t = Transform({"tz":3}) # 3D translation
   5 a.transform(t) # ERROR is thrown

A more in depth look at the dictionary constructor

The dictionary constructor, which is equivalent to calling the default constructor followed by the set_params function, takes up to 9 parameters as exemplified in the following 

   1 t = Transform({"type":"eman","az":10,"alt":150,"phi":20,"scale":2.0,"mirror":True,"tx":3.4,"ty":3,"tz":2})
   2 t = Transform({"type":"spider","phi":10,"theta":150,"psi":20,"scale":2.0,"mirror":True,"tx":3.4,"ty":3,"tz":2})

If any of the angles or not specified they are implicitly set to 0 

   1 t = Transform({"type":"spider","phi":10,"scale":2.0,"mirror":True,"tx":3.4,"ty":3,"tz":2}) # spider theta and psi are both 0
   2 t = Transform({"type":"spider","scale":2.0,"mirror":True,"tx":3.4,"ty":3,"tz":2}) # spider phi, theta and psi are all 0

If no euler type is specified then the rotation matrix is the identity 

   1 t = Transform({"scale":2.0,"mirror":True,"tx":3.4,"ty":3,"tz":2}) # Rotation matrix is the identity

Similarly if any of the translation parameters are not specified they are implicitly set to 0 

   1 t = Transform({"scale":2.0,"mirror":True,"tx":3.4,"ty":3}) # tz is 0
   2 t = Transform({"scale":2.0,"mirror":True}) # tx,ty and tz are all 0

If scale is not specified it is by default 1.0, similarly if mirror is not specified it is be default False 

   1 t = Transform({"tx":3.4,"ty":3,"tz":3}) # scale is 1.0, mirror is False

A more in depth look at set_params

Constructing a Transform with some dictionary is the same as calling set_params on a Transform that is the identity. 

   1 d = {"type":"eman","az":10,"alt":150,"phi":20,"scale":2.0,"mirror":True,"tx":3.4,"ty":3,"tz":2}
   2 t = Transform(d) # t is initialized as the identity and then set_params(d) is called internally
   3 s = Transform() # s is the identity
   4 s.set_params(d) # s is identical to t

The main difference between calling set_params explicitly on a Transform as opposed to constructing a Tranform with a dictionary lies in the fact that the construction method first sets the Transform object to the identity before calling set_params. So if calling the set_params function on a Transform that has already been initialized and had many things done than you should be aware of the following...

If unspecified, old parameters are retained

   1 t = Transform({"type":"eman","az":10,"alt":150,"phi":20,"scale":2.0,"mirror":True,"tx":3.4,"ty":3,"tz":2})
   2 d = {"tx":23,"ty":23,"tz":12}
   3 t.set_params(d) # t still has the same rotation, scale and mirror but it has an updated translation

For rotation and translation, setting one is equivalent to setting them all

   1 t = Transform({"tx":3.4,"ty":3,"tz":2})
   2 d = {"tx":23}
   3 t.set_params(d) # ty and tz are now 0
   4 #
   5 t = Transform({"type":"eman","az":10,"alt":150,"phi":20})
   6 d = {"type":"eman","phi":10}
   7 t.set_params(d) # alt and az are 0
   8 t.set_params({"type":eman}) # all angles are now 0

EMAN2/TransformInPython (last edited 2023-09-29 12:51:26 by SteveLudtke)