Contents
Quick Summary
Supported symmetries in EMAN2/SPARX are :
- Cn - single rotational n-fold symmetry axis
- Dn - dihedral rotational n-fold, eg - GroEL is ~D7
- icos - icosahedral, (5,3,2)
- oct - octahedral, symmetry of a cube (4,3,2)
- tet - tetrahedral, (3,2)
- h - helical
Introduction
This page will describe how EMAN2 defines the asymmetric unit, and its associated mirror portion, for each of the symmetries. This is mostly important in the context the the projection tools (EMAN1: project3d, EMAN2: e2project3d.py) which project quasi-uniformly over the asymmetric unit for each of the symmetries, generating the reference images for particle classification.
A symmetric object is often defined by its symmetric axes and how they are arranged with respect to one another. For each symmetry one may define a set of affine transformations (i.e. rotations), which when applied to the symmetric object yield it in exactly equivalent (but unique) orientation. These will be referred to as the set of rotational symmetry operations, the total in number of which is the same as the overall symmetry of the object. For instance the 60-fold symmetric icosahedral symmetry has a total of 60 rotational symmetry operations (including the identity). Similarly the 14-fold symmetric D7 symmetry has 14 and so on.
Similar to the rotational symmetry operations, the total number of asymmetric units will match the overall symmetry of the object. The asymmetric unit of a symmetric 3D object can be defined in many ways. In one regard, it is the 3D subvolume of the entire 3D object that an asymmetric object can exist inside of, in each of the asymmetric units, in equivalent orientation, without destroying the overall symmetry of the object, that is, applying a rotational symmetry must yield the 3D object in indentical conformation.
In single particle reconstruction we must project over this asymmetric unit as accurately as possible. To do this we often think in terms of the unit sphere and imagine it as encapsulating the symmetric object. We isolate a single asymmetric unit and define the surface of the unit sphere we must uniformly project through to ensure the sampling of the single asymmetric unit in all of its unique orientations.
This seems simple enough, but depending on the approach, we must also consider the influence of mirror (or reflective) symmetry which occurs when we generate a projection from the opposite side of the hemisphere. Take this idea one step futher, if it is true that a projection from one side of the hemisphere is the mirror of the projection from the opposite side, then if we apply the correct rotational symmetry operation, the mirror projection must exist in same asymmetric unit that produced the equivalent "un mirrored" projection. In fact it is true that exaclty half of the projections over the asymmetric unit are the mirror projections of the other half.
In EMAN1 it was imperative that the mirror portion of the asymmetric unit was accurately demarcated. This was due to EMAN1's approach which used two rounds of classification for each reconstruction, one using the raw (unmodified) particle data, and one where the particle data was mirrored. The particle was then classified to which projection it exhibited the greatest similarity toward, based on the best results of the two runs. In EMAN2 the equivalent approach of projecting over the entire asymmetric unit (including the mirrored portion) but doing only one round of classification will be available to the user.
This document will therefore describe the way in which EMAN2 demarcates the entire and mirror portions of the asymmetric unit, for each of the symmetries.
Cn symmetry
C-symmetry occurs when an object is symmetric about a single axis. The degree of symmetry about this axis is referred to as n. A rotation of 2pi/n about this axis will yield the object in an identical (but unique) conformation. Based on this fact it is possible to define the asymmetric unit for c-symmetries as shown in Figure 1 (left). However, as stated above, half of the asymmetric unit will contain the mirror projections of the other half, and the way in which the mirror projections are arranged respectfully in the asymmetric unit depends on whether n is even or odd. To illustrate this, the behavior of even and odd mirror projections in the asymmetric unit is shown in Figure 1 (middle and right, respectfully).
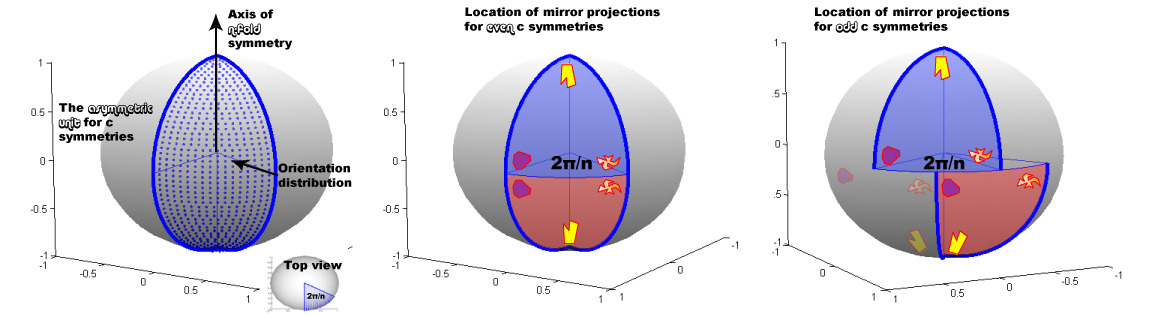
Figure 1. C-symmetry in EMAN: The asymmetric unit and location of mirror projections for even and odd n.
Dn symmetry
An object with d-symmetry is similar to an object c-symmetry in that a rotation around the n-fold axis of symmetry will yield the object in an identical conformation. In addition to this the d-symmetric object exhibits (potentially numerous) 2-fold symmetries in the equatorial domain. These 2-fold axes of symmetry are mutually separated by an angle of 2pi/n and the number of 2-fold symmetric axes a d-symmetric object exhibits is dependent on whether n is even or odd, and is n/2 or n, respectfully. The asymmetric unit of d-symmetric objects is defined in terms of the n-fold and 2-fold axes of symmetry and is shown in Figure 2 (left). Similar to the behavior of the asymmetric unit for c-symmetries, in d-symmetries the behavior of the mirror projections is dependent on whether n is even or odd as shown in Figure 2 (middle and right, respectfully).
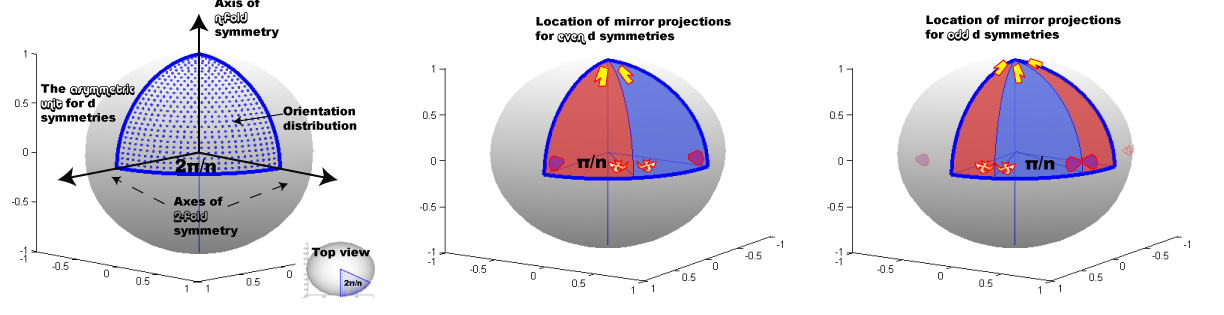
Figure 2. D-symmetry in EMAN: The asymmetric unit and location of mirror projections for even and odd n.
If the mirror portion of the asymmetric unit is to be taken into account From Figure 2 it becomes clear that one must be careful when defining the asymmetric unit for odd D symmetries. The table below details the location of the 2 fold symmetric axis/axes when examining the distribution of orientations in D-symmetry asymmetric units. Note the for D6 symmetry the implication is that n=12 etc (for D7 n=14).
Symmetry |
Location of 2 fold axes on equator (azimuthal angle in degrees) |
Odd C, no mirror |
360/(2*n) |
Even C, no mirror |
0 |
Odd D, include mirror |
360/(2*n) and 3*360/(2*n) |
Even D, include mirror |
0, 360/(n/2) |
Platonic symmetries
Although there are 5 Platonic solids in all, for the purposes of single particle reconstruction both the the cube/octahedron and the icosahedron/dodecahedron pairs can be considered equivalent. Therefore here we will restrict our vocabulary to include only the tetrahedron, octahedron and icosahedron, but note for the material presented her, cube and dodecahedron are interchangeable for octahedron and icosahedron, respectively. The discussion here is meant to be brief, however for a detailed description of platonic symmetry see Baldwin & Penczek (2007).
A tetrahedron is an example of a platonic solid that has 4 3-fold axes of symmetry and 3 2-fold axes of symmetry. The asymmetric unit of the tetrahedron is defined in terms of neighboring 3- and 2-fold axis of symmetry and is depicted graphically in Figure 3 (left). The octahedron has 3 4-fold axes of symmetry, 4 3-fold axes of symmetry, and 6 2-fold axes of symmetry and its asymmetric unit (with respect to neighboring symmetric axes) is shown in Figure 3 (middle). Similarly, the icosahedron has 6 5-fold, 10 3-fold and 15 2-fold axes of symmetry and its asymmetric unit is shown (with respect to neighboring symmetric axes) in Figure 3 (right).
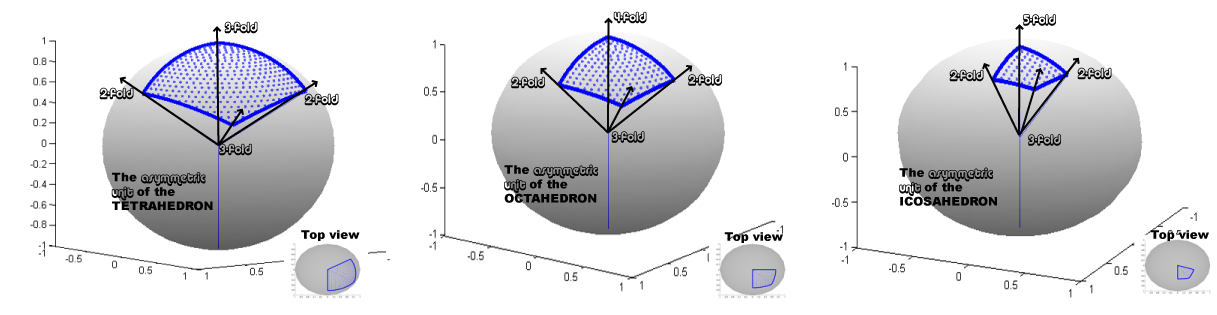
Figure 3. The asymmetric unit of the platonic solids (tetrahedron, octahedron, icosahedron).
The mirror portion of the tetrahedral asymmetric is perhaps the most unusual and is shown graphically in terms of the neighboring symmetric axes in Figure 4 (left). This is in contrast to the mirror projection behavior of octahedral and icosahedral symmetries which is shown in Figure 4 (right).
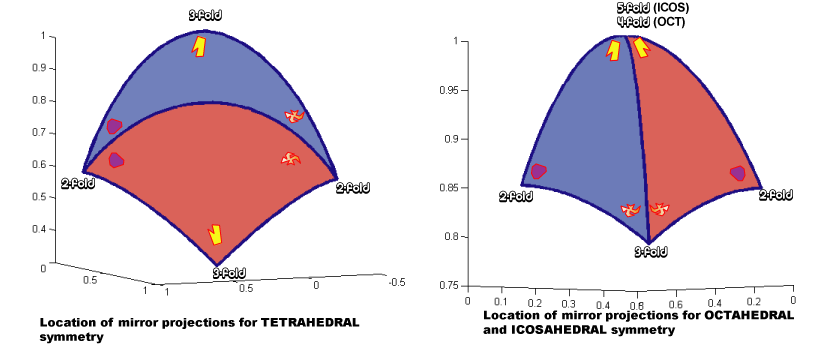
Figure 4. Location of mirror projections in the asymmetric unit of the tetrahedron, octahedron and icosahedron.
Helical Symmetry
To generate the symmetry-related elements with helical symmetry involves simultaneously rotating around the Z axis and translating along the Z axis to the next symmetric position. Additionally, there can be a C symmetry present within the overall helix, and this is also included in the helical symmetry specification. This C symmetry is specified with nstart. For the helical repeat, you specify daz, the rotation about the Z axis and tz, the translation along the Z axis.
Since helical symmetry extends infinitely along the Z axis, it would be difficult to impose on any real object unless we take into account that we are looking at only a small fragment of the infinite helix. This gives us an additional parameter 'nsym', which is the number of helical repeats to generate along +Z and -Z. For example, if one had a box size of 256, and tz was 16, then an nsym of 8 should be sufficient (+8 and -8 are covered).
The final optional maxtilt parameter is used when generating projections of an object for projection matching. Normally projections would be made for 'side views' of the helix. If maxtilt>0, then projections of tilted filaments will also be generated, up to the specified tilt angle.
The specification is:
H<nsym>:<nstart>:<daz in degrees>:<tz in pixels>[:<maxtilt>] for example: H8:2:17.3:14.2
Interactive asymmetric unit viewing using emimag3dsym.py in EMAN2
EMAN2 includes a tool that will display the asymmetric unit of each of the symmetries in an interactive OpenGL interface. The distribution of projection orientations within the asymmetric unit is also shown. Pictures of this interface are shown below.
|
|
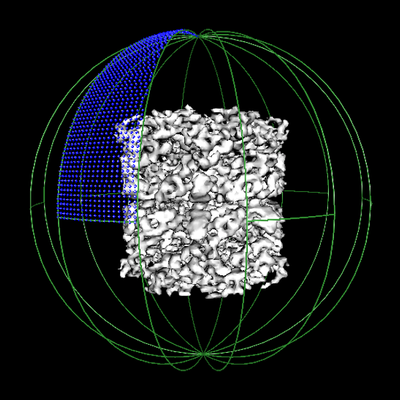
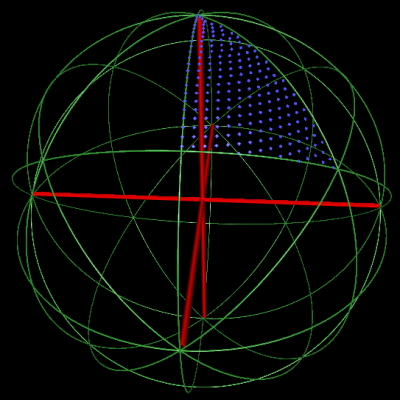
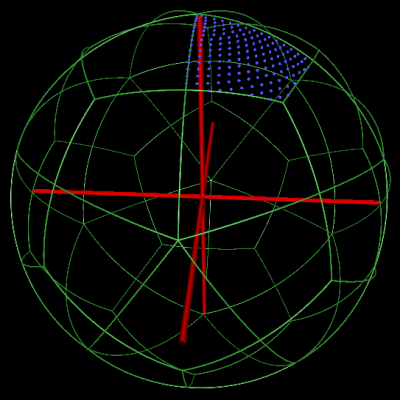
The asymmetric unit of GroEL, including the mirror portion, with projection orientations distributed at 1.2 degrees |
The asymmetric unit of GroEL excluding its mirror portion |
Below similar snapshots are shown for the Platonic symmetries.
|
|
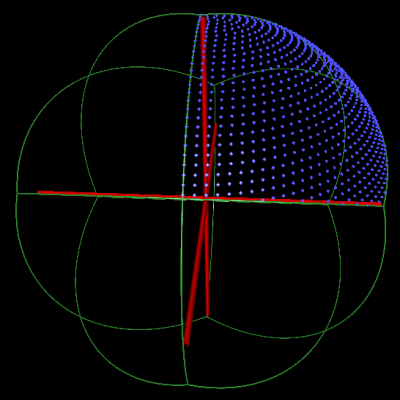
Tetrahedral asymmetric unit |
Tetrahedral asymmetric unit without mirror orientations |
|
|
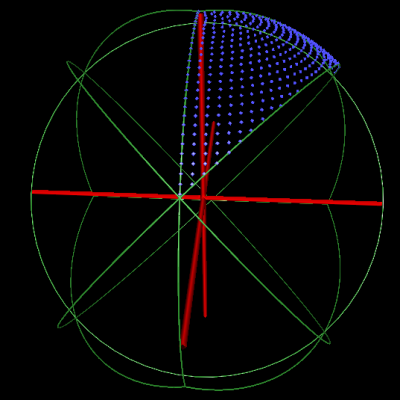
Octahedral asymmetric unit |
Octahedral asymmetric unit without mirror orientations |
|
|
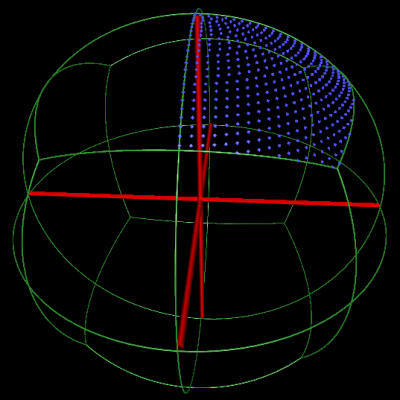
Icosahedral asymmetric unit |
Icosahedral asymmetric unit without mirror orientations |
Python Programs Making use of Symmetry
The Symmetry3D object in EMAN2's library represents a symmetry generator. The easiest way to construct one of these objects is through the parsesym function which is part of the core library you get when you from EMAN2 import *". sym=parsesym("c4"), for example, will return a symmetry object representing the C4 symmetry group as described above. The symmetry object has a number of different useful methods: sym.gen_orientations(orientgen,parms) - Will generate a list of Transform objects filling one asymmetric unit using the specified parameters. sym.get_nsym() - will return the symmetry number (ie- 60 for icos, 14 for D7, etc.) sym.get_sym(n) - will return the nth symmetry operator for this symmetry. The first operator (n=0) will be the identity matrix (no rotation). reduce(xform,n) - will return the the Transform Use References
e2help.py orientgen -v 2 for details